鋁板幕墻計算方法（第三部分）

   L: B板短邊長度:0.400m

   t: 板厚度: 2.5mm

   E: 彈性模量: 70000.000N/mm2

   v: 泊松比: 0.330

   D: 板彎曲剛度:

   D=E×t3/12/(1-v2)/100000

    =1.023

   板撓度:

   U=104×f1×Wk×L4×η/D

    =2.281mm

   板撓度與邊長比值:

   Du=U/L/1000

     =0.006

   0.006≤1/100   B板撓度可以滿足要求    

三、C板強(qiáng)度校核:    

   校核依據(jù)：σ=M/W=6×m×q×L2×η/t2≤fa=80.000N/mm2

   Lx: C板寬度: 1.200m

   Ly: C板高度: 0.400m

   L: C板短邊長: 0.400m

   t: 金屬板厚度: 2.5mm

   Wk: 風(fēng)荷載標(biāo)準(zhǔn)值: 1.987kN/m2

   垂直于平面的分布水平地震作用:

   qEAk: 垂直于幕墻平面的分布水平地震作用 (kN/m2)

   qEAk=5×αmax×GAK

       =5×0.160×67.500/1000

       =0.054kN/m2

   荷載設(shè)計值為：

   q=1.4×Wk+1.3×0.5×qEAk

    =2.817kN/m2

   m1: 跨中彎矩系數(shù), 按短邊與長邊的邊長比(0.400/1.200=0.333)

       查表得: 0.072

   m0: 固端彎矩系數(shù), 按短邊與長邊的邊長比(0.400/1.200=0.333)

       查表得: 0.084

   θ=(Wk+0.5×qEAk)×L4×109/Et4

     =18.86

   η: 折減系數(shù)，按θ=18.86

       查表得:0.91

   C板所受的最大彎矩應(yīng)力值為:

    =28.428N/mm2

   28.428N/mm2≤80.000N/mm2  強(qiáng)度可以滿足要求    

   C板撓度校核:

   校核依據(jù): ｆ/L≤1/100

   f1: 撓度系數(shù),  按短邊與長邊的邊長比(0.400/1.200=0.333)

       查表得: 0.003

   Wk: 風(fēng)荷載標(biāo)準(zhǔn)值: 1.987kN/m2

   Lx: C板寬度: 1.200m

   Ly: C板高度: 0.400m

   L: C板短邊長: 0.400m

   t: 板厚度: 2.5mm

   E: 彈性模量: 70000.000N/mm2

   v: 泊松比: 0.330

   D: 板彎曲剛度:

   D=E×t3/12/(1-v2)/100000

    =1.023

   板撓度:

   U=104×f1×Wk×L4×η/D

    =1.181mm

   板撓度與邊長比值:

   Du=U/L/1000

     =0.003

   0.003≤1/100   C板撓度可以滿足要求    

四、支座處強(qiáng)度校核:    

1.支座處校核依據(jù)：根據(jù)一根肋兩側(cè)相鄰兩板格的支承情況，先求肋兩側(cè)的固端彎矩系數(shù)，平均后為此處彎矩系數(shù)：

      m支=(m支(i)+m支(j))/2

   校核依據(jù)：σ=M/W=6×m支×q×L2×η/t2≤fa=80.000N/mm2

2.支座強(qiáng)度校核：

   B,C 之間：

      肋側(cè)B板格固端彎矩系數(shù)=0.121

      肋側(cè)C板格支座彎矩系數(shù)=0.084

      支座彎矩系數(shù):m=(mbx+mcx)/2

                =0.103KN·m

   σ=6×m支×q×L2×103×η/t2

     =40.456N/mm2

   40.456N/mm2≤80.000N/mm2  強(qiáng)度可以滿足要求

五、加強(qiáng)肋校核:    

 1. 強(qiáng)度校核:

   校核依據(jù)：σ=M/W=6×m×q×L2×η/t2≤fa=85.500N/mm2

   Lx: B板寬度: 1.200m

   Ly: B板長度: 0.400m

   t: 加強(qiáng)肋厚度: 3.0mm

   Gw: 加強(qiáng)肋寬度: 35.000mm

   Gh: 加強(qiáng)肋高度: 35.000mm

   加強(qiáng)肋彎矩:

   M=q×Ly×Lx2/8

    =2.817×0.400×1.2002/8

    =0.203kN·m

   加強(qiáng)肋抗彎矩:

   W=(Gw×Gh3-(Gw-2×t)×(Gh-2×t)3)/6/Gh/103

    =3.778cm3

   加強(qiáng)肋抗彎矩為:3.778cm3

   γ: 承載能力調(diào)整系數(shù): 1.05

   加強(qiáng)肋強(qiáng)度:

   σ=M×103/1.05/W

     =51.130N/mm2

   51.130N/mm2≤85.500N/mm2

   加強(qiáng)肋強(qiáng)度可以滿足要求    

 2. 加強(qiáng)肋剛度校核:

   校核依據(jù):ｆ=5qL4/384EI   ｆ/L≤1/100

   E: 彈性模量: 70000.000N/mm2

   加強(qiáng)肋慣性矩:

   I=(Gw×Gh3-(Gw-2×t)×(Gh-2×t)3)/12/104

    =6.611cm4

   加強(qiáng)肋慣性矩為:6.611cm4

   加強(qiáng)肋撓度:

   U=5×108×qK×Ly×Lx4/384/E/I

    =5×108×2.014×0.400×1.2004/384/70000/6.611

    =4.700mm

   肋撓度與邊長比值:

   Du=U/Lx/1000

     =0.00392

   0.004≤1/100   加強(qiáng)肋撓度可以滿足要求    

六、固定片（壓板）計算    

    Wfg_x: 計算單元總寬為1200.0mm

    Hfg_y: 計算單元總高為1200.0mm

    Hyb1: 壓板上部分高為350.0mm

    Hyb2: 壓板下部分高為350.0mm

    Wyb: 壓板長為20.0mm

    Hyb: 壓板寬為35.0mm

    Byb: 壓板厚為5.0mm

    Dyb: 壓板孔直徑為5.0mm

    Wk: 作用在幕墻上的風(fēng)荷載標(biāo)準(zhǔn)值為1.987(kN/m2)

    qEAk: 垂直于幕墻平面的分布水平地震作用為0.054(kN/m2)(不包括立柱與橫梁傳來的地震作用)

    A: 每個壓板承受作用面積(m2)

    A=(Wfg_x/1000/2)×(Hyb1+Hyb2)/1000/2

     =(1.2000/2)×(0.3500+0.3500)/2

     =0.2100 (m2)

    Pwk: 每個壓板承受風(fēng)荷載標(biāo)準(zhǔn)值(KN)

    Pwk=Wk×A=1.987×0.2100=0.417(KN)

    Pw: 每個壓板承受風(fēng)荷載設(shè)計值(KN)

    Pw=1.4×Pwk=1.4×0.417=0.584(KN)

    Mw: 每個壓板承受風(fēng)荷載產(chǎn)生的最大彎矩(KN.m)

    Mw=1.5×Pw×(Wyb/2)=1.5×0.584×(0.0200/2)=0.009 (KN.m)

    Pek: 每個壓板承受地震作用標(biāo)準(zhǔn)值(KN)

    Pek=qEAK×A=0.054×0.2100=0.011(KN)

    Pe: 每個壓板承受地震作用設(shè)計值(KN)

    Pe=1.3×Pek=1.3×0.011=0.015(KN)

    Me: 每個壓板承受地震作用產(chǎn)生的最大彎矩(KN.m)

    Me=1.5×Pe×(Wyb/2)=1.5×0.015×(0.0200/2)=0.000 (KN.m)

    采用Sw+0.5Se組合

    M: 每個壓板承受的最大彎矩(KN.m)

    M=Mw+0.5×Me=0.009+0.5×0.000=0.009(KN.m)

    W: 壓板截面抵抗矩(mm3)

    W=((Hyh-Dyb)×Byb2)/6

     =((35.0-5.0)×5.02)/6

     =125.0 (mm3)

    I: 壓板截面慣性矩(mm4)

    I=((Hyh-Dyb)×Byb3)/12

     =((35.0-5.0)×5.03)/12

     =312.5 (mm4)

   σ=106×M/W=106×0.009/125.0=71.0 (N/mm2)

   σ=71.0(N/mm2) ≤ 84.2(N/mm2)強(qiáng)度滿足要求    

   U: 壓板變形(mm)

   U=1.5×1000×2×(Pwk+0.5×Pek)×Wyb3/(48×E×I)

    =1.5×1000×(0.417+0.5×0.011)×20.03/(24×0.7×105×312.5)

    =0.005mm

   Du: 壓板相對變形(mm)

   Du=U/L=U/(Wyb/2)=0.005/10.0=0.0005

   Du=0.0005≤1/180 符合要求    

   Nvbh: 壓板螺栓(受拉)承載能力計算(N):

   D: 壓板螺栓有效直徑為4.250(mm)

   Nvbh=(π×D2×170)/4=(3.1416×4.2502×170)/4

       =2411.7 (N)

   Nvbh=2411.7≥2×(Pw+0.5×Pe)=1183.1(N)滿足要求    

七、幕墻立柱計算    

幕墻立柱按簡支梁力學(xué)模型進(jìn)行設(shè)計計算：

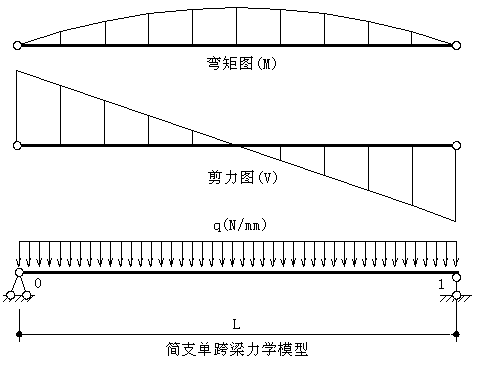
1. 荷載計算:

(1)風(fēng)荷載均布線荷載設(shè)計值(矩形分布)計算

    qw: 風(fēng)荷載均布線荷載設(shè)計值(kN/m)

    W: 風(fēng)荷載設(shè)計值: 2.536kN/m2

    B: 幕墻分格寬: 1.200m

    qw=W×B

     =2.536×1.200

     =3.044 kN/m

(2)地震荷載計算

   qEA: 地震作用設(shè)計值(KN/m2):

   GAk: 幕墻構(gòu)件(包括面板和框)的平均自重: 450N/m2

  垂直于幕墻平面的均布水平地震作用標(biāo)準(zhǔn)值:

   qEAk: 垂直于幕墻平面的均布水平地震作用標(biāo)準(zhǔn)值 (kN/m2)

   qEAk=5×αmax×GAk

       =5×0.160×450.000/1000

       =0.360 kN/m2

   γE: 幕墻地震作用分項系數(shù): 1.3

   qEA=1.3×qEAk